Curiosity and Skepticism: A Healthy Mindset
Contents
2. Curiosity and Skepticism: A Healthy Mindset#
This chapter is focused on helping you develop a healthy mindset, or mental attitude, for scientific investigation. This mindset is composed of two opposing modes of operation: curiosity and skepticism.
Learning Objectives In this chapter, you will learn:
the dual modes of curiosity and skepticism 1
Running Example: Detective Enola
This book is full of examples of curiosity and skepticism in action. But before we introduce any of the detailed scientific case studies, let’s use the scenario of a detective story for this chapter: The owner of a large fortune has just been found in her manor with a knife in her back, and Detective Enola Knox suspects a family member is responsible. As we’ll see below, the protagonist of a murder mystery exemplifies the dual modes of curiosity and skepticism.
2.1. Using a Scientific Mindset Rather Than Following a Procedure#
Curiosity and skepticism are not a fixed procedure, but rather two modes of a mindset. The subjects of the following sections are not a checklist to go through sequentially, but rather a set of “moves” or approaches we can employ during the scientific investigative process.
An analogy: The U.S. legal system is based on the idea that truth can be found by pitting two rational opposing forces against each other. Through the defense and prosecution teams working against each other, presenting evidence, and finding holes in each other’s arguments, society can come closer to the truth and hence justice.
The back-and-forth between curiosity and skepticism is similar: two modes we should switch between during scientific investigations. By engaging in curious behavior, we can ask questions and pose tentative answers. By engaging in skepticism, we can identify flaws and improve our analysis. In practice, we should move between the two modes iteratively throughout an investigative process, as this will improve our analysis and uncover flaws (Figure 2.1). Let’s look at these two modes in greater detail.
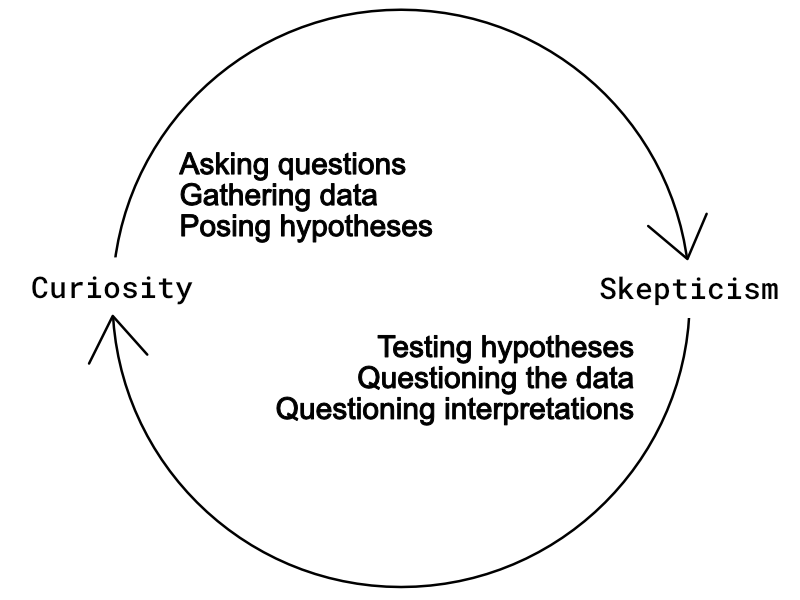
Fig. 2.1 The dual modes of curiosity and skepticism, with their associated “moves.”#
2.2. Curiosity#
The mode of curiosity is characterized by openness: to exploration, to new questions, to other approaches, and to possible answers. Some of the “moves” in the curious mode are (1) asking questions, (2) gathering data, and (3) posing hypotheses.
2.2.1. Asking questions#
The very notion of curiosity is closely associated with asking questions: We describe a child as “curious” if they tend to ask a lot of questions. Most scientific investigations start with some sort of overarching question that kicks off a research effort—we will call this a modeling question. However, the process of asking questions doesn’t stop there. The process of scientific inquiry tends to involve posing new questions in an iterative manner.
Tip
Running Example: Detective Knox. In a murder mystery, a detective will generally have one overarching question: “Whodunit?” But to answer this driving question, Enola will have to pose and answer a variety of subordinate questions: Who are the suspects? What facts do I know? Why is the eldest son being cagey? These questions can help the detective decide what data to gather next.
2.2.2. Gathering data#
Questions are useful in part because they focus our efforts. One of the main ways we make progress in answering our questions is to gather data.
In scientific modeling, we can gather both experimental data (from a physical experiment) and simulated data (from a simulation of a model). Experimental data requires running a physical experiment. Experiments require time and hardware but come directly from reality. Lightweight computational models can be run far more quickly to suggest possible trends, which can help to plan physical experiments.
Note that we can gather data in a curious exploratory way or in a more skeptical testing fashion. The data collection we plan in the curious mode tends to be more ad hoc. Perhaps we plan out a quick pilot study or obtain some archival data that is only somewhat associated with our question. The point of gathering data in the curious mode is not to be comprehensively formal; rather, it is to move quickly and refine our questions so we can move toward the greater clarity of a formal hypothesis.
Tip
Running Example: Detective Knox. Even before Detective Knox formulates an answer to any of her initial questions, she will try a variety of “moves” to gather data for her investigation. She might try dusting for prints at the scene of the crime, interviewing eyewitnesses to search for plausible motives, or sending the murder weapon out to the lab for a forensic test. For Detective Knox, the coroner’s examination of the victim’s body provides a time of death, information about blunt trauma to the face, and a knife-wound as the cause of death, all of which narrow the set of possible suspects—hence the possible hypotheses.
2.2.3. Posing hypotheses#
The primary output of the curious mode is a testable hypothesis. This is a synthesis of the available data and initial questions, one which ideally addresses our original modeling question. Arriving at a hypothesis is often the inflection point to move from the curious mode to the skeptical mode.
Posing a hypothesis requires interpreting the data. This is where domain-specific knowledge of the problem is essential: Only a specialist in your field can interpret the data in terms of your discipline’s accepted conventions. However, regardless of one’s discipline, there is one criterion that all hypotheses must meet—a scientific hypothesis must be testable.
As Popper [2005] wrote on the philosophy of science, a scientific hypothesis should be specific enough to be falsifiable; that is, able to be shown to be false. Falsifiability is a reasonable criterion for determining what is a testable hypothesis. If a hypothesis is too flexible or too vague to be testable, this is a sign that the hypothesis needs refinement. Usually, a falsifiable hypothesis makes predictions about what would happen under a certain experimental setting; in this case, the hypothesis would be falsified if the prediction failed to hold.
Tip
Running Example: Detective Knox. Detective Knox wants to know “whodunit,” so her hypothesis should include a suspect, motive, and opportunity. She suspects the eldest son is responsible, as the household staff intimated that he is greedy and impatient to inherit. She makes sure to incorporate all the data she has gathered in formulating her hypothesis; she thinks the son stabbed his mother in the back with a knife around the time of death, causing her to fall forward onto her face.
2.3. Skepticism#
The mode of skepticism is characterized by rejection: rejecting hypotheses, finding flaws in the data and methods, and even probing the importance of questions. Some of the “moves” in the skeptical mode include (1) testing hypotheses, (2) questioning the data, and (3) questioning the interpretation. Let’s look at each of these in turn.
2.3.1. Testing hypotheses#
Once we have posed a hypothesis, it needs to be subjected to testing. As noted under “Posing hypotheses” above, any scientific hypotheses must be testable, usually by being falsifiable. However, you might not recognize your hypothesis as untestable until you switch over to the skeptical mode.
Remember, a skeptic would not use a “friendly” test. Try to formulate a strenuous test of your hypothesis. What would a worst-case scenario look like for your hypothesis? What would be a convincing argument, even to your toughest critic?
We’ll see more about this in Section 8.2, but as a preview, you should use data that are independent of your exploratory data to test a hypothesis. In the parlance of machine learning, testing a model on the same data that was used to train it is an optimistic (and even foolish!) way to assess a model [James et al., 2013]. If your hypothesis is true, then your findings should hold for an independently-gathered dataset.
Warning
Running Example: Detective Knox. Detective Knox is confident in her hypothesis, so she accuses the son. However, he denies the accusation and produces a compelling alibi: He was with the butler during the victim’s time of death, and the butler is beyond reproach. Clearly, something about Detective Knox’s hypothesis does not hold up.
If your hypothesis does not hold, then you need to reexamine your reasoning. This includes both your data and your interpretation of the facts.
2.3.2. Questioning the data#
Sometimes the data themselves are in error, either in the values recorded or in the context of the data. Simulations can be misconfigured or unconverged, which will lead to errors in the data values. Experiments can have confounding (aka lurking) variables, which will lead to an incorrect understanding of the data context. When your hypothesis does not hold, you must hunt down and eliminate these kinds of issues.
Conversations with a Model: Confounding Variables
Gianluca. “What is a confounding variable?”
Bot. “A confounding variable is an extraneous variable that affects the relationship between the independent variable and the dependent variable in a study. Confounding variables can make it difficult to determine the true relationship between the variables of interest.
For example, imagine a study that seeks to examine the relationship between coffee consumption and heart disease. However, if the study participants who drink more coffee also tend to smoke cigarettes more frequently, it may be difficult to determine whether the observed relationship between coffee consumption and heart disease is due to the coffee or the smoking. In this case, smoking would be considered a confounding variable.”
As we will see in Chapter 6, uncertainty can be either real or erroneous, with respect to a target quantity. Real uncertainty affects the quantity we aim to study, while erroneous uncertainty affects only our measurement. Determining whether the uncertainty we see is due to real or erroneous sources helps us narrow our search to either before or after the phenomenon of interest. If there is an explanation for erroneous uncertainty, then our measurement is subject to a mistake that we can eliminate. Collecting new data while eliminating such sources of erroneous uncertainty will help us more accurately understand the object of our scientific study.
Warning
Running Example: Detective Knox. Detective Knox thinks there may be something fishy about the reported time of death, so she has a longer conversation with the coroner. A closer inspection of the victim’s body confirms the time of death, so the data do not seem to be in error….
2.3.3. Questioning interpretations#
Sometimes it’s not the data that are in error, but rather our interpretation. This can mean we made an error in our reasoning, or that we were missing some key facts about the scenario at hand.
If we see unexpected variation in our measurements that seems to arise from some consistent phenomena, we might find that a previously unknown phenomenon can explain this behavior 2. Such anomalous variability can lead to a scientific discovery. However, a lack of variability can also lead to scientific advancement.
Before Einstein formulated his theory of relativity in the early 1900s, all waves had been observed to travel within some medium. Hence, scientists at the time believed that light, exhibiting wavelike properties, must travel within a medium called the luminiferous aether. Scientists such as Albert Michelson carried out experiments to detect the “aether wind” due to the motion of Earth through this “aether” but failed to detect any change in the speed of light. Einstein’s contribution overturned this understanding of physics, and our modern understanding is that light travels through a vacuum at a speed constant to all observers.
Tip
Running Example: Detective Knox. In conversation with the coroner, Detective Knox realizes that the knife wound and face trauma could have occurred at very different times. If the victim were killed at one time and her body clumsily moved later, this could account for both wounds. Upon further investigation, she finds a cunning mechanism hidden in the victim’s chair: The mother died by a deadly trap while the son was with the butler, and the son returned later to rearrange the scene to make it appear to be a much simpler murder. By employing both curiosity and skepticism, Detective Knox solved the case.
2.4. Using the Mindset to Reduce Uncertainty#
This book is focused on modeling in the presence of uncertainty. Using a mindset that switches between curiosity and skepticism will help you reduce uncertainty to a tolerable level: Curiosity will help you steer your process, while skepticism will help you arrive at sound conclusions. Iterating between these modes until the uncertainty is tolerable will help you reach an answer to your modeling questions.
2.5. Practicing the Mindset#
These ideas about curiosity and skepticism are important, but if they remain only ideas they are just theoretical. You need to go beyond simply knowing about these ideas and start using them in your own scientific practice. However, this is easier said than done!
To help you make use of the curious and skeptical modes, the case studies in this book are written to emphasize these modes. With a bit of imagination, you can generalize these sorts of insights to your own context. While reading this book, think about ways the same kinds of observations or issues could show up in your scientific investigations. Better yet, try practicing some of the techniques suggested in this book on your own problems!
- 1
We are grateful to Bill Behrman, who first introduced Zach to the idea of curiosity and skepticism as modes of operation. These dispositions are also discussed by Wild and Pfannkuch [1999].
- 2
We will see an example of lurking variables and the techniques used to detect them in Section 9.2.